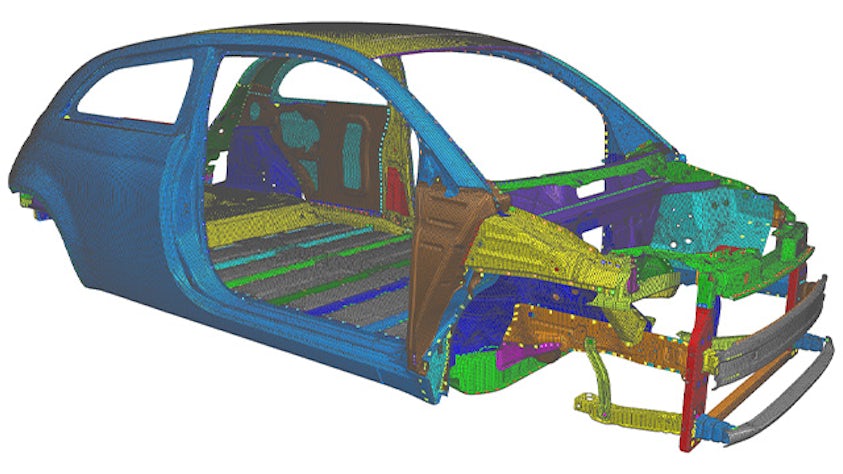
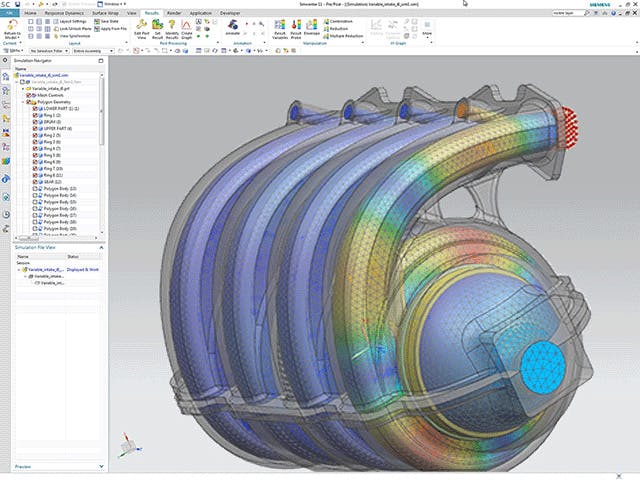
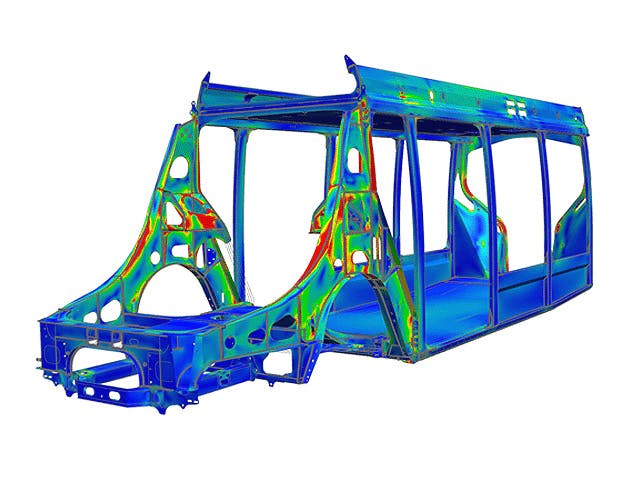
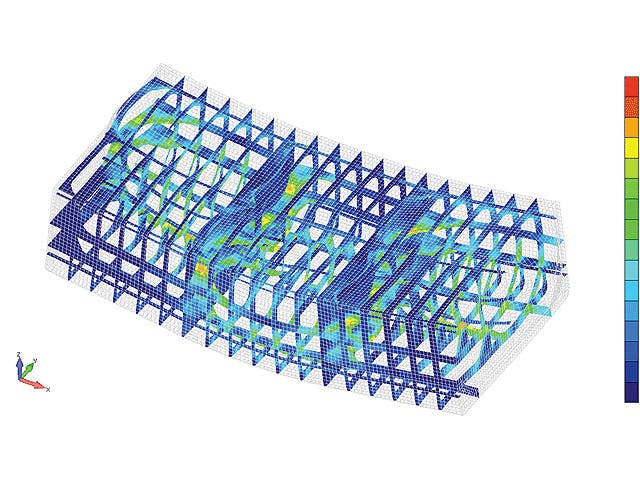
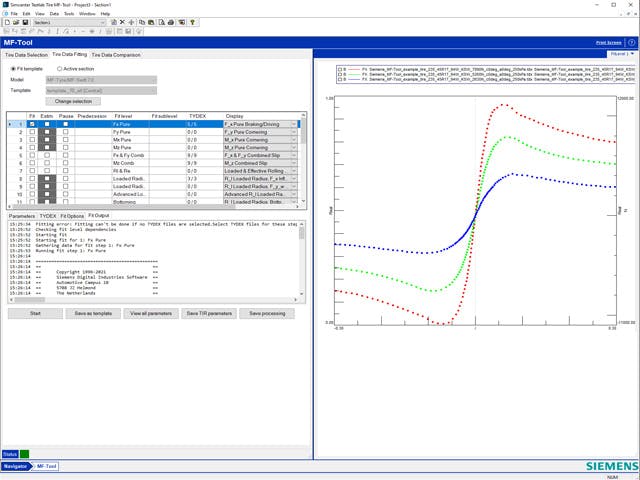
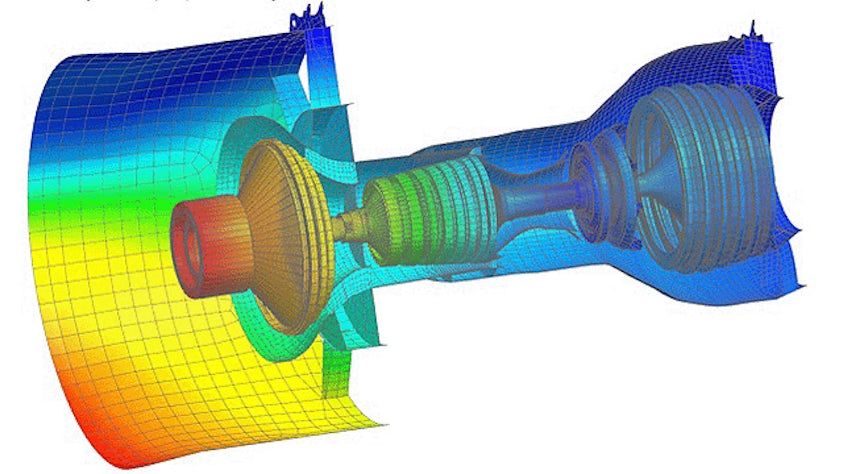
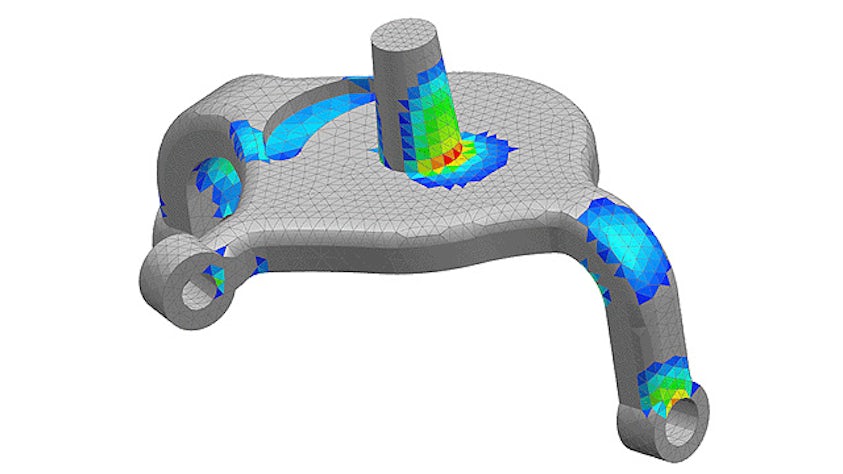
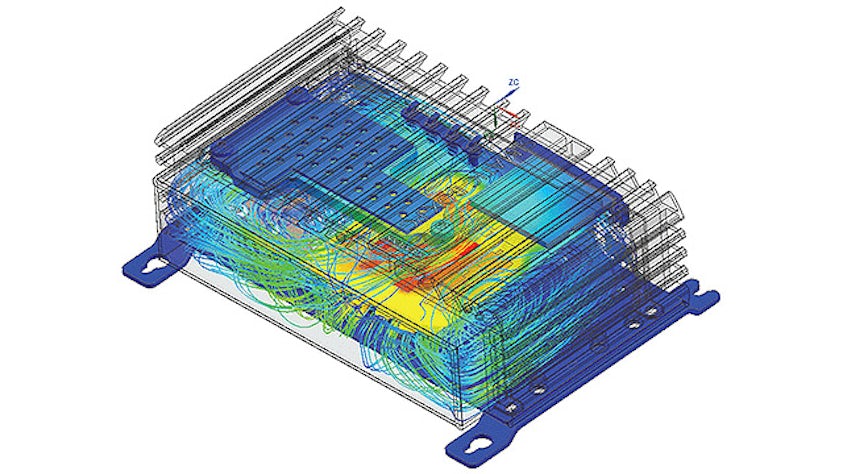
The simulation process includes steps for model preparation, often called pre-processing, and results analysis, often called post-processing. Pre-processing steps include importing, defeaturing and cleaning up computer-aided design (CAD) geometry, creating the finite element (FE) mesh, defining loads and boundary conditions as well as solution parameters. Pre-processing is often the longest, most time-consuming step in the simulation process.
Simcenter offers the tools you need to reduce the time you spend preparing analysis models and spend more time evaluating results. Quickly move from multi-CAD geometry data to a complete, run-ready analysis model using unique tools for computer-aided engineering (CAE) geometry editing, comprehensive meshing, FE assembly management, multi-CAE solver environments, and fast simulation results post-processing and reporting. Efficiently pre- and post-process your simulation models quickly for accurate and fast simulation solvers so you can spend more time engineering innovation.